Vectors on the exam in mathematics. Actions on vectors. Vectors for dummies. Actions with vectors. Vector coordinates. The simplest problems with vectors Vectors theory formulas

Standard definition: "A vector is a directed line segment." This is usually the limit of a graduate's knowledge of vectors. Who needs some kind of "directed segments"?
But in fact, what are vectors and why are they?
Weather forecast. "Wind northwest, speed 18 meters per second." Agree, the direction of the wind (where it blows from) and the module (that is, the absolute value) of its speed also matter.
Quantities that have no direction are called scalars. Mass, work, electric charge are not directed anywhere. They are characterized only by a numerical value - “how many kilograms” or “how many joules”.
Physical quantities that have not only an absolute value, but also a direction are called vector quantities.
Speed, force, acceleration - vectors. For them, it is important "how much" and it is important "where". For example, the free fall acceleration is directed towards the Earth's surface, and its value is 9.8 m/s 2 . Momentum, electric field strength, magnetic field induction are also vector quantities.
You remember that physical quantities are denoted by letters, Latin or Greek. The arrow above the letter indicates that the quantity is a vector:
Here is another example.
The car is moving from A to B. The end result is its movement from point A to point B, i.e. movement by a vector  .
.

Now it is clear why a vector is a directed segment. Pay attention, the end of the vector is where the arrow is. Vector length is called the length of this segment. Designated: or
So far, we have been working with scalar quantities, according to the rules of arithmetic and elementary algebra. Vectors are a new concept. This is another class of mathematical objects. They have their own rules.
Once upon a time, we didn’t even know about numbers. Acquaintance with them began in elementary grades. It turned out that numbers can be compared with each other, added, subtracted, multiplied and divided. We learned that there is a number one and a number zero.
Now we get to know vectors.
The concepts of "greater than" and "less than" do not exist for vectors - after all, their directions can be different. You can only compare the lengths of vectors.
But the concept of equality for vectors is.
Equal are vectors that have the same length and the same direction. This means that the vector can be moved parallel to itself to any point in the plane.
single is called a vector whose length is 1 . Zero - a vector whose length is equal to zero, that is, its beginning coincides with the end.
It is most convenient to work with vectors in a rectangular coordinate system - the one in which we draw function graphs. Each point in the coordinate system corresponds to two numbers - its x and y coordinates, abscissa and ordinate.
The vector is also given by two coordinates:
Here, the coordinates of the vector are written in brackets - in x and in y.
They are easy to find: the coordinate of the end of the vector minus the coordinate of its beginning.

If the vector coordinates are given, its length is found by the formula

Vector addition
There are two ways to add vectors.
one . parallelogram rule. To add the vectors and , we place the origins of both at the same point. We complete the parallelogram and draw the diagonal of the parallelogram from the same point. This will be the sum of the vectors and .

Remember the fable about the swan, cancer and pike? They tried very hard, but they never moved the cart. After all, the vector sum of the forces applied by them to the cart was equal to zero.
2. The second way to add vectors is the triangle rule. Let's take the same vectors and . We add the beginning of the second to the end of the first vector. Now let's connect the beginning of the first and the end of the second. This is the sum of the vectors and .

By the same rule, you can add several vectors. We attach them one by one, and then connect the beginning of the first to the end of the last.

Imagine that you are going from point A to point B, from B to C, from C to D, then to E and then to F. The end result of these actions is a move from A to F.
When adding vectors and we get:
![]()
Vector subtraction
The vector is directed opposite to the vector . The lengths of the vectors and are equal.
Now it is clear what subtraction of vectors is. The difference of the vectors and is the sum of the vector and the vector .

Multiply a vector by a number
Multiplying a vector by a number k results in a vector whose length is k times different from the length . It is codirectional with the vector if k is greater than zero, and directed oppositely if k is less than zero.

Dot product of vectors
Vectors can be multiplied not only by numbers, but also by each other.
The scalar product of vectors is the product of the lengths of vectors and the cosine of the angle between them.

Pay attention - we multiplied two vectors, and we got a scalar, that is, a number. For example, in physics mechanical work is equal to the scalar product of two vectors - force and displacement:
![]()
If the vectors are perpendicular, their dot product is zero.
And this is how the scalar product is expressed in terms of the coordinates of the vectors and:
From the formula for the scalar product, you can find the angle between the vectors:

This formula is especially convenient in stereometry. For example, in problem 14 profile exam in mathematics, you need to find the angle between intersecting lines or between a line and a plane. Problem 14 is often solved several times faster than the classical one.
In the school curriculum in mathematics, only the scalar product of vectors is studied.
It turns out that, in addition to the scalar, there is also a vector product, when a vector is obtained as a result of multiplying two vectors. Who passes the exam in physics, knows what the Lorentz force and the Ampère force are. The formulas for finding these forces include exactly vector products.
Vectors are a very useful mathematical tool. You will be convinced of this in the first course.

DEFINITION
Vector(from lat. " vector"-" bearing") - a directed segment of a straight line in space or on a plane.
Graphically, a vector is depicted as a directed straight line segment of a certain length. The vector whose beginning is at the point and the end at the point is denoted as (Fig. 1). Also, a vector can be denoted by a single small letter, for example, .
If a coordinate system is given in space, then the vector can be uniquely specified by a set of its coordinates. That is, a vector is understood as an object that has a value (length), direction and application point (beginning of the vector).
The beginnings of vector calculus appeared in works in 1831 in the works German mathematician, mechanics, physicist, astronomer and surveyor Johann Carl Friedrich Gauss (1777-1855). Works on operations with vectors were published by the Irish mathematician, mechanician and theoretical physicist, Sir William Rowan Hamilton (1805-1865) as part of his quaternion calculus. The scientist proposed the term "vector" and described some operations on vectors. Vector calculus got its further development thanks to the work on electromagnetism of the British physicist, mathematician and mechanic James Clerk Maxwell (1831-1879). In the 1880s, the book "Elements of Vector Analysis" by the American physicist, physicochemist, mathematician and mechanic Josiah Willard Gibbs (1839-1903) was published. Modern vector analysis was described in 1903 by the English self-taught scientist, engineer, mathematician and physicist Oliver Heaviside (1850-1925).
DEFINITION
Length or vector module is the length of the directed segment that defines the vector. Designated as .

Basic types of vectors
Zero vector is called a vector whose start point and end point are the same. The length of the null vector is zero.
Vectors that are parallel to the same line or lie on the same line are called collinear(Fig. 2).
co-directional if their directions are the same.
In Figure 2, these are the vectors and . The co-direction of vectors is denoted as follows: .
Two collinear vectors are called opposite directions if their directions are opposite.
In figure 3, these are the vectors and . Designation: .
1. What is a vector?
2. Addition of vectors.
3. Equality of vectors.
4. Scalar product of two vectors and its properties.
5. Properties of operations on vectors.
6. Proofs and problem solving.
One of the fundamental concepts of modern mathematics is the vector and its generalization - the tensor. The evolution of the concept of a vector was carried out due to the wide use of this concept in various fields of mathematics, mechanics, as well as in technology.
The end of the past and the beginning of the current century were marked by the extensive development of vector calculus and its applications. Vector algebra and vector analysis, a general theory of vector space were created. These theories were used in the construction of special and general relativity, which play an extremely important role in modern physics.
As required new program in mathematics, the concept of a vector has become one of the leading concepts of the school mathematics course.
What is a vector? Oddly enough, the answer to this question presents certain difficulties. There are various approaches to the definition of the concept of a vector; Moreover, even if we confine ourselves to the elementary-geometric approach to the concept of a vector, which is the most interesting for us here, then even then there will be different views on this concept. Of course, whatever definition we take, a vector - from an elementary geometric point of view - is a geometric object characterized by a direction (i.e., a straight line specified up to parallelism and a direction on it) and a length. However, such a definition is too general, not causing specific geometric representations. According to this general definition, a parallel translation can be considered a vector. Indeed, one could accept such a definition: “A vector is any parallel translation”. This definition is logically flawless, and on its basis the whole theory of actions on vectors can be built and applications of this theory can be developed. However, this definition, despite its complete concreteness, cannot satisfy us here either, since the idea of a vector as a geometric transformation seems to us insufficiently clear and far from physical ideas about vector quantities.
So, vector called the family of all parallel to each other, equally directed and having the same length segments (Fig. 1).
The vector is depicted in the drawings as a segment with an arrow (i.e., not the entire family of segments, which is a vector, is depicted, but only one of these segments). Bold Latin letters are used to designate vectors in books and articles. a, b, c and so on, and in notebooks and on the board - Latin letters with a dash on top , The same letter, but not bold, but light (and in the notebook and on the board, the same letter without a dash) denotes the length of the vector. The length is sometimes also indicated by vertical lines - as the module (absolute value) of the number. Thus, the length of the vector a denoted by a or I a I, and in handwritten text, the length of the vector a denoted by a or I a I. In connection with the representation of vectors in the form of segments (Fig. 2), it should be remembered that the ends of the segment representing the vector are unequal: one end of the segment to the other.
Distinguish between the beginning and the end of a vector (more precisely, a segment representing a vector).
Quite often, the concept of a vector is given another definition: a directed segment is called a vector. In this case, vectors (i.e. directed segments) having the same length and the same direction (Fig. 3) are agreed to be considered equal.
Vectors are said to be equally directed if their half-lines are equally directed.
Addition of vectors.
All of the above does not yet make the concept of a vector meaningful and useful enough. The concept of a vector gets more content and a rich possibility of applications when we introduce a kind of “geometric arithmetic” - the arithmetic of vectors, which allows us to add vectors, subtract them and perform a number of other operations on them. We note in this connection that, after all, the concept of a number becomes interesting only with the introduction of arithmetic operations, and not in itself.
The sum of vectors a and in with coordinates a 1, a 2 and a 1, a 2 called vector with with coordinates a 1 + into 1, a 2 + into 2, those. a(a 1; a 2) + in(in 1 ;in 2) = with(a 1 + in 1; a 2 + in 2).Consequence:
To prove the commutativity of vector addition on the plane, we need to consider an example. a and in - vectors (Fig. 5).
Let be
1. We build a parallelogram OASV: AM II OB, VN II OA.
To prove the associativity, we set aside from an arbitrary point O the vector OA = a, from point A vector AB = in and from point to - vector sun = s. Then we have: AB + BC = AC.
whence follows the equality a + (in + with) = (a + b)+ p. Note that the above proof does not use the drawing at all. This is typical (with some skill) for solving problems using vectors. Let us now consider the case when the vectors a and in directed in opposite directions and equal lengths; such vectors are called opposite. Our rule of vector addition leads to the fact that the sum of two opposite vectors is a "vector" that has zero length and no direction; this “vector” is represented by a “segment of zero length”, i.e. dot. But this is also a vector, which is called zero and is denoted by the symbol 0.
Vector equality.
Two vectors are said to be equal if they are combined by a parallel translation. This means that there is a parallel translation that moves the beginning and end of one vector to the beginning and end of another vector, respectively.
From this definition equality of vectors implies that different vectors are equally directed and equal in absolute value.
And vice versa: if the vectors are equally directed and equal in absolute value, then they are equal.
Indeed, let the vectors AB and With D - identically directed vectors, equal in absolute value (Fig. 6). A parallel transfer that takes point C to point A combines the half-line CD with the half-line AB, since they are equally directed. And since the segments AB and CD are equal, then the point D is aligned with the point B, that is, the parallel transfer translates the vector CD to vector AB. So the vectors AB and With D are equal, which was to be proved.There will also be tasks for independent solution to which you can see the answers.
Vector concept
Before you learn all about vectors and operations on them, tune in to solve a simple problem. There is a vector of your enterprise and a vector of your innovative abilities. The vector of entrepreneurship leads you to Goal 1, and the vector of innovative abilities - to Goal 2. The rules of the game are such that you cannot move in the directions of these two vectors at once and achieve two goals at once. Vectors interact, or, speaking mathematically, some operation is performed on vectors. The result of this operation is the "Result" vector, which leads you to Goal 3.
Now tell me: the result of which operation on the vectors "Enterprise" and "Innovative abilities" is the vector "Result"? If you can't say right away, don't be discouraged. As you study this lesson, you will be able to answer this question.
As we have seen above, the vector necessarily comes from some point A in a straight line to some point B. Consequently, each vector has not only a numerical value - length, but also a physical and geometric - direction. From this the first, simplest definition of a vector is derived. So, a vector is a directed segment going from a point A to the point B. It is marked like this:

And to start different vector operations , we need to get acquainted with one more definition of a vector.
A vector is a kind of representation of a point to be reached from some starting point. For example, a three-dimensional vector is usually written as (x, y, z) . Simply put, these numbers represent how far you have to go in three different directions to get to the point.
Let a vector be given. Wherein x = 3 (right hand points to the right) y = 1 (left hand points forward) z = 5 (under the point there is a ladder leading up). From this data, you will find the point by walking 3 meters in the direction indicated by the right hand, then 1 meter in the direction indicated by the left hand, and then a ladder awaits you and, climbing 5 meters, you will finally find yourself at the end point.
All other terms are refinements of the explanation presented above, necessary for various operations on vectors, that is, for solving practical problems. Let's go through these more rigorous definitions, dwelling on typical vector problems.
Physical examples vector quantities can be the displacement of a material point moving in space, the speed and acceleration of this point, as well as the force acting on it.

geometric vector represented in two-dimensional and three-dimensional space in the form directed segment. This is a segment that has a beginning and an end.
If a A is the beginning of the vector, and B is its end, then the vector is denoted by the symbol or a single lowercase letter . In the figure, the end of the vector is indicated by an arrow (Fig. 1)
Length(or module) of a geometric vector is the length of the segment that generates it
The two vectors are called equal , if they can be combined (when the directions coincide) by parallel translation, i.e. if they are parallel, point in the same direction and have equal lengths.
In physics, it is often considered pinned vectors, given by the application point, length, and direction. If the point of application of the vector does not matter, then it can be transferred, keeping the length and direction to any point in space. In this case, the vector is called free. We agree to consider only free vectors.
Linear operations on geometric vectors

Multiply a vector by a number
Vector product per number A vector is called a vector that is obtained from a vector by stretching (at ) or shrinking (at ) times, and the direction of the vector is preserved if , and reversed if . (Fig. 2)
It follows from the definition that the vectors and = are always located on one or parallel lines. Such vectors are called collinear. (You can also say that these vectors are parallel, but in vector algebra it is customary to say "collinear".) The converse is also true: if the vectors and are collinear, then they are related by the relation
Therefore, equality (1) expresses the condition of collinearness of two vectors.

Vector addition and subtraction
When adding vectors, you need to know that sum vectors and is called a vector , the beginning of which coincides with the beginning of the vector , and the end - with the end of the vector , provided that the beginning of the vector is attached to the end of the vector . (Fig. 3)

This definition can be distributed over any finite number of vectors. Let in space given n free vectors . When adding several vectors, their sum is taken as the closing vector, the beginning of which coincides with the beginning of the first vector, and the end with the end of the last vector. That is, if the beginning of the vector is attached to the end of the vector, and the beginning of the vector to the end of the vector, etc. and, finally, to the end of the vector - the beginning of the vector, then the sum of these vectors is the closing vector ![]() , whose beginning coincides with the beginning of the first vector , and whose end coincides with the end of the last vector . (Fig. 4)
, whose beginning coincides with the beginning of the first vector , and whose end coincides with the end of the last vector . (Fig. 4)
The terms are called the components of the vector, and the formulated rule is polygon rule. This polygon may not be flat.
When a vector is multiplied by the number -1, the opposite vector is obtained. The vectors and have the same length and opposite directions. Their sum gives null vector, whose length is zero. The direction of the null vector is not defined.
In vector algebra, there is no need to consider the operation of subtraction separately: to subtract a vector from a vector means to add the opposite vector to the vector, i.e. ![]()
Example 1 Simplify the expression:
![]() .
.
 ,
,
that is, vectors can be added and multiplied by numbers in the same way as polynomials (in particular, also problems for simplifying expressions). Usually, the need to simplify linearly similar expressions with vectors arises before calculating the products of vectors.
Example 2 The vectors and serve as diagonals of the parallelogram ABCD (Fig. 4a). Express in terms of and the vectors , , and , which are the sides of this parallelogram.

Decision. The intersection point of the diagonals of a parallelogram bisects each diagonal. The lengths of the vectors required in the condition of the problem are found either as half the sums of the vectors that form a triangle with the desired ones, or as half the differences (depending on the direction of the vector serving as a diagonal), or, as in the latter case, half the sum taken with a minus sign. The result is the vectors required in the condition of the problem:

There is every reason to believe that you now correctly answered the question about the "Enterprise" and "Innovative abilities" vectors at the beginning of this lesson. Correct answer: these vectors are subjected to an addition operation.
Solve problems on vectors on your own, and then look at the solutions
How to find the length of the sum of vectors?
This problem occupies a special place in operations with vectors, as it involves the use of trigonometric properties. Let's say you have a task like the following:
Given the length of vectors ![]() and the length of the sum of these vectors . Find the length of the difference of these vectors .
and the length of the sum of these vectors . Find the length of the difference of these vectors .
Solutions to this and other similar problems and explanations of how to solve them - in the lesson " Vector addition: the length of the sum of vectors and the cosine theorem ".
And you can check the solution of such problems on Online calculator "Unknown side of a triangle (vector addition and cosine theorem)" .
Where are the products of vectors?
The products of a vector by a vector are not linear operations and are considered separately. And we have lessons "Dot Product of Vectors" and "Vector and Mixed Product of Vectors".
Projection of a vector onto an axis
The projection of a vector onto an axis is equal to the product of the length of the projected vector and the cosine of the angle between the vector and the axis:
![]()
As is known, the projection of a point A on the line (plane) is the base of the perpendicular dropped from this point to the line (plane).

Let - an arbitrary vector (Fig. 5), and and - projections of its beginning (points A) and end (points B) per axle l. (To build the projection of a point A) draw straight through the point A plane perpendicular to the line. The intersection of a line and a plane will determine the required projection.
Component of the vector on the l axis called such a vector lying on this axis, the beginning of which coincides with the projection of the beginning, and the end - with the projection of the end of the vector .
The projection of the vector onto the axis l called a number
![]() ,
,
equal to the length of the component vector on this axis, taken with a plus sign if the direction of the component coincides with the direction of the axis l, and with a minus sign if these directions are opposite.
The main properties of vector projections on the axis:
1. The projections of equal vectors on the same axis are equal to each other.
2. When a vector is multiplied by a number, its projection is multiplied by the same number.
3. The projection of the sum of vectors on any axis is equal to the sum of the projections on the same axis of the terms of the vectors.
4. The projection of a vector onto an axis is equal to the product of the length of the projected vector and the cosine of the angle between the vector and the axis:
![]()
 .
.

Decision. Let's project the vectors onto the axis l as defined in the theoretical reference above. From Fig.5a it is obvious that the projection of the sum of vectors is equal to the sum of the projections of vectors. We calculate these projections:

We find the final projection of the sum of vectors:
Relationship of a vector with a rectangular Cartesian coordinate system in space
Acquaintance with rectangular Cartesian coordinate system in space took place in the corresponding lesson, preferably open it in a new window.
In an ordered system coordinate axes 0xyz axis Ox called x-axis, axis 0y – y-axis, and axis 0z – applicate axis.

with arbitrary point M space tie vector
called radius vector points M and project it onto each of the coordinate axes. Let us denote the values of the corresponding projections:
Numbers x, y, z called coordinates of point M, respectively abscissa, ordinate and applique, and are written as an ordered point of numbers: M(x; y; z)(Fig. 6).
A vector of unit length whose direction coincides with the direction of the axis is called unit vector(or ortom) axes. Denote by
Accordingly, the unit vectors of the coordinate axes Ox, Oy, Oz
![]()
Theorem. Any vector can be decomposed into the unit vectors of the coordinate axes:

![]() (2)
(2)
Equality (2) is called the expansion of the vector along the coordinate axes. The coefficients of this expansion are the projections of the vector onto the coordinate axes. Thus, the expansion coefficients (2) of the vector along the coordinate axes are the coordinates of the vector.
After choosing a certain coordinate system in space, the vector and the triple of its coordinates uniquely determine each other, so the vector can be written in the form
The vector representations in the form (2) and (3) are identical.
The condition of collinear vectors in coordinates
As we have already noted, vectors are called collinear if they are related by the relation
Let vectors ![]() . These vectors are collinear if the coordinates of the vectors are related by the relation
. These vectors are collinear if the coordinates of the vectors are related by the relation
![]() ,
,
that is, the coordinates of the vectors are proportional.
Example 6 Given vectors ![]() . Are these vectors collinear?
. Are these vectors collinear?
Decision. Let's find out the ratio of the coordinates of these vectors:
![]() .
.
The coordinates of the vectors are proportional, therefore, the vectors are collinear, or, what is the same, parallel.
Vector length and direction cosines
Due to the mutual perpendicularity of the coordinate axes, the length of the vector
![]()
is equal to the length of the diagonal of a rectangular parallelepiped built on the vectors
and is expressed by the equality
![]() (4)
(4)
A vector is completely defined by specifying two points (beginning and end), so the coordinates of the vector can be expressed in terms of the coordinates of these points.
Let the beginning of the vector in the given coordinate system be at the point
and the end is at the point


From equality
Follows that
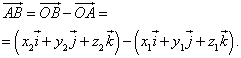
or in coordinate form
Hence, the coordinates of the vector are equal to the differences of the coordinates of the same name of the end and beginning of the vector . Formula (4) in this case takes the form
The direction of the vector is determined direction cosines . These are the cosines of the angles that the vector makes with the axes Ox, Oy and Oz. Let's designate these angles respectively α , β and γ . Then the cosines of these angles can be found by the formulas
The direction cosines of a vector are also the coordinates of the vector's vector and thus the vector's vector

![]() .
.
Considering that the length of the vector vector is equal to one unit, that is,
![]() ,
,
we get the following equality for the direction cosines:
Example 7 Find the length of a vector x = (3; 0; 4).
Decision. The length of the vector is
![]()
Example 8 Given points:
Find out if the triangle built on these points is isosceles.
Decision. Using the vector length formula (6), we find the lengths of the sides and find out if there are two of them equal:

Two equal sides have been found, so there is no need to look for the length of the third side, and the given triangle is isosceles.
Example 9 Find the length of a vector and its direction cosines if ![]() .
.
Decision. The vector coordinates are given:
![]() .
.
The length of the vector is equal to the square root of the sum of the squares of the vector's coordinates:
![]() .
.
Finding direction cosines:

Solve the problem on vectors yourself, and then look at the solution
Operations on vectors given in coordinate form
Let two vectors and given by their projections be given:
![]()
![]()
Let us indicate actions on these vectors.
Reading time 8 minutes
Modern psychology and psychiatry are no longer limited to classical scientific theories. Disputes and discussions about the truth and objectivity of popular concepts have been going on for centuries, psychological research is constantly being carried out, the purpose of which is to come to the only true result. But besides this, new alternative currents are increasingly appearing, well-known theories are being modified, the teachings of world minds of psychology and psychiatry are being transformed, such as the professional psychoanalyst Sigmund Freud or his no less famous colleague Carl Gustav Jung. In this article, we will focus on just such a new trend, which has made a real revolution in Russian psychology, is called system-vector psychology. You will learn what it is, what is the main idea of this direction, and you will also be able to get acquainted in detail with each of the 8 presented vectors and even independently determine your own personality type.
Ideas of system-vector psychology
To begin with, it is worth saying that system-vector psychology is not a generally accepted trend in modern scientific circles. Some particularly ardent adherents of classical ideas even call this direction "network pseudoscience." But, like any other theory, the psychological concept of eight vectors not only has the possibility of existence, it even managed to acquire its own army of adherents. As the founder of the system-vector theory V.K. Tolkachev said:
The universe is large enough and inexhaustible, which makes it possible to find confirmation of any theory in it. ©
System-vector psychology did not arise from scratch. The theories of Sigmund Freud were taken as a basis, later refined by Vladimir Ganzen and completed by his student Viktor Tolkachev.
In 1908, the psychoanalyst Freud's article "Character and Anal Erotica" saw the world, in which the psychoanalyst concludes that character traits are directly related to human erogenous zones. The publication caused a wide resonance, numerous followers of the Freudian idea appeared. One of them at the end of the 20th century was Viktor Konstantinovich Tolkachev, a psychologist from St. Petersburg. He developed a typology of characters associated with such areas as the eyes, mouth, nose and ears. According to V. K. Tolkachev, he was inspired to develop and refine the theory of Sigmund Freud by the book “Systemic Descriptions in Psychology” by Academician Vladimir Aleksandrovich Ganzen.
The origin and development of the teachings of Viktor Tolkachev
V. K. Tolkachev developed a holistic psychological concept for determining the type of personality using vectors. With the help of the concept of "vector" and a detailed analysis of 8 characteristic types, a theory called "Applied System-Vector Psychoanalysis" was born. Tolkachev has been conducting various trainings, seminars and lectures on this issue for more than 30 years. Thanks to one of his first students, Mikhail Borodyansky, a special test was developed that assesses the individual potential that each of the vectors has, and allows you to determine the personal type of character in relation to the system-vector psychology of eight vectors (Tolkachev-Borodyansky test). Now there are many followers of the vector system who continue to conduct psychological trainings and seminars. The most famous Internet coach in this area is Yuri Burlan.
What is the essence of system-vector psychology
During the development of psychology as a science, many different personality typologies have been developed. These are typologies according to Jung or according to Gannushkin, Erich Fromm proposed his classification. Multiple tests have been developed to determine psychological type individual, for example, the Szondi test or the common 16Personalities. In fact, V. K. Tolkachev, like many of his predecessors, proposed his own version of identifying a personality type.
System-vector psychology is positioned not as a branch of classical psychology or a certain trend, but as a separate science of studying personality typology. A vector is a symbiosis of physiological and psychological qualities, such as, for example, character, temperament, health, habits of the individual and other similar properties. In fact, the vector is the center of pleasure. The vectors are associated with a specific hole on the human body, which is at the same time erogenous zone. Each personality may have several vectors (from 1 to 8, in practice, the largest number of vectors present is the number 5).
The presence of a vector determines the number and degree of human aspirations and needs for self-realization, aimed at obtaining pleasure. The inability to implement the existing vector, according to the developers of the theory, leads to depression and a feeling of dissatisfaction, which makes it impossible for a person to achieve inner harmony with his "I".
Vector steps (quartels) of personality development
System-vector psychology identifies 8 main vectors in personality typology. Namely: visual, skin, sound, muscle, oral, olfactory, urethral and anal vectors. They are located in four main quartels (steps) that form the way of life of a person.
The principle of the arrangement of vectors:
- Information stage. Answer sound ( inner part quartels) and visual (outer part) vectors. At this stage, the process of development and self-knowledge of the individual takes place.
- Energy stage. The oral (outer part) and olfactory (inner part) vectors are responsible. The purpose of this stage is to predetermine the place of the individual in the social system, the construction of a clear hierarchy.
- Time step. Respond anal (inner space of the quarter) and urethral (outer space) vectors. Temporary division of life into stages: past and future. At this stage, there is the acquisition and processing of experience from past generations, as well as the desire for progress and development of society.
- Spatial step. The muscle (inner part) and skin (outer part of the quartel space) vectors are responsible. The stage responsible for the physical shell is the labor realization of a person, the use of physical strength, etc.
Characterization of vectors
A more detailed vector characteristic looks like this:
- skin vector. People with a vivid manifestation of this type are pronounced extroverts. They realize themselves on the spatial level. The main direction of kozhnikov is the protection of territories.
- muscle vector. Introverts. The type of thinking is practical and visual-effective. The main direction is hunting, participation in hostilities.
- anal vector. Introverts with systems thinking. Typical occupations for the owners of the anal vector are the protection of the hearth, the accumulation and transmission of information from previous generations.
- urethral vector. 100% extroverts. They have out-of-the-box thinking. Born Tactics. The life purpose of people with a pronounced urethral vector is to be leaders, commanders in chief, leaders.
- visual vector. Extroverts with a figurative type of intelligence. They are at the information stage of development. Main activity: protection of territories (during the day).
- Sound vector. Absolute introverts with an abstract type of thinking. Activity: protection of territories in the dark.
- oral vector. Representatives of this type are mostly extroverts. They have an inherent verbal method of thinking. Main occupation: organization of events (in peacetime), danger warning (during hostilities).
- Olfactory vector. Introverts, characterized by an intuitive type of thinking, prefer non-verbal ways of conveying information. The main direction: intelligence, drawing up strategies.
System-vector psychology divides vectors into more important, so to speak, basic ones, and those that are of lesser value in the development of a personality. The olfactory, urethral and sound vectors are dominant, they dominate the other vectors. These three vectors do not overlap with other available ones, and also cannot be eradicated by external social factors, such as upbringing or social system.
Each individual himself determines which vectors are the main ones in the psychotype of his personality. For each vector, even such characteristics as certain external data, psychic features inherent in a particular vector archetype have been developed. Each of the eight vectors is assigned a specific geometric shape and color.
The vectors are also divided into lower (urethral, anal, muscular and skin) and upper (visual, sound, olfactory and oral). System-vector psychology shows that the lower vectors are responsible for libido, human sexual desires, while the upper vectors are looking for a connection with the spiritual world. The upper vectors are available to absolutely every person, in contrast to the lower ones, which not all personal archetypes are endowed with.
System-vector psychology: its purpose
There is not a single person who is able to refuse pleasure; even religion itself has to justify the demand to give up pleasures in the near future with the promise of incomparably greater and more valuable joys in the other world. © Sigmund Freud
What is eight vector psychology for? What is its function and benefit to humans?
The main goal of vector psychology is to know yourself and enjoy life using your internal vectors. This system is aimed at self-knowledge of the individual, determining his role in society, in order to avoid moral dissatisfaction with himself and his life. If a person cannot realize himself in society, does not know his true needs and desires, then a constant feeling of dissatisfaction can lead to a depressive state.
System-vector psychology is also aimed at revealing the sexual desires and needs of a person. Can be used as professionally oriented tests.
The psychological theory, developed by Viktor Tolkachev on the basis of Freud's postulates, allows you to discover the secrets of the subconscious, to realize what exactly is the driving force of a person, the root cause of all his actions and deeds. The benefit of studying the vectors of system-vector psychology is also in building communication links with people around you: employees, relatives, friends. If two people have the same vectors, then often this is the key to friendly relations. And vice versa - the contrast of vectors explains the incompatibility in couples and the hostility of individuals to each other. In the words of the unwitting founder of this doctrine, Sigmund Freud:
We do not choose each other by chance ... We meet only those who already exist in our subconscious. ©
System-vector psychology is not proven or absolutely true. This is just one of the methodologies for identifying certain type personality. The amount of criticism by experienced specialists regarding the teachings of V. K. Tolkachev proves the imperfection of this psychological concept. Discussions and disputes do not subside between adherents of classical psychology and Tolkachev's students.
The former tend to consider the vector approach to personality determination as sectarian and hypnotic-obsessive (supposedly, trainings on teaching this technique are carried out exclusively for commercial purposes). The latter sincerely believe in the objectivity of system-vector psychology and prove its benefits for individuals and humanity as a whole. To learn more about the theses and concepts of this doctrine, you can watch the video of Yuri Burlun's introductory lectures on the system of vectors. Only by bringing together a complete picture of the doctrine, each person will be able to independently draw a conclusion about the truth of the ideas put forward.
